Understanding Angles - Calculating Polygons
Calculating Polygons
Polygon calculations come up frequently in woodworking. Finding the angles and dimensions of used in building multi-sided frames, barrels and drums (to name a few applications) begins with an understanding to the geometry of regular (symmetrical) polygons.
Regular Polygon Shapes
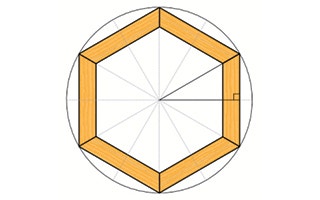
In most cases, to build a polygon shape, you'll need to know the bevel or miter angle necessary to join the sides. To do that, you'll need to use trigonometric functions in conjunction with a basic property of the polygon shape. A regular polygon is an example of a complex shape that can be thought of as the splicing together of a number of right triangles. Specifically, a regular polygon with N sides can be divided into N * 2 "fundamental" right triangles. The 6-sided polygon in Figure 1, for example, can be divided into 12 equally proportioned right triangles. The lines that form two sides of each triangle also cut through the center of the circle that circumscribes the polygon. Because the lines divide the circle into equal sections, we know that each triangle will have one acute angle equal to 360/(N * 2).
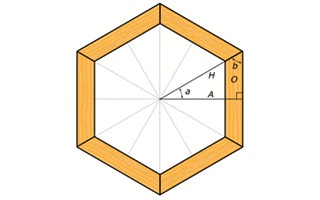
Calculating the Bevel or Miter Angle of the Parts
For angle a of triangle AOH in Figure 2: a = 360/(6 * 2) =>a = 30 degrees Angle b of triangle AOH is the complement of angle a: b = 90 - 30 =>b = 60 degrees The saw setting necessary to cut the bevel or miter where the joints meet will be either angle a or angle b, depending on the calibration system of the saw you are using. Cutting the beveled edge of barrel or drum staves on a table saw will almost always require you to set the saw at angle a, because nearly all table saw bevel angle scales are calibrated to treat a straight up and down vertical setting of the blade as a 0 degree setting. The same would hold true if you are cutting the parts for a multi-sided frame on a miter saw. Most table saw miter gauges, on the other hand, treat a square cut as a 90 degree setting, making angle b the correct angle setting.
Calculating the Dimensions of a Polygon
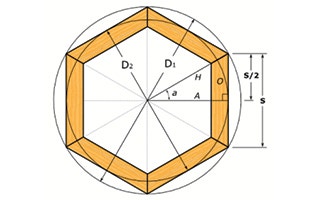
So far, we know the how to calculate the acute angles that make up the fundamental right triangles of a polygon with N sides. Now, using that information, we can find the dimensions of the parts we'd need to cut to build a polygon shape, based on the overall dimensions of the polygon or, if we wanted to, calculate the overall dimensions of the shape based on the dimension of the sides of the polygon. If we begin with dimension D1 of the diameter of the circle that circumscribes the entire shape and work toward finding the length of the sides, we can begin the calculations by noticing that the length of side H of the fundamental right triangle of every polygon is equal to the overall dimension D1 divided by 2, and also that the length of side O of the triangle is equal to length of the sides divided by 2. Knowing that, we can use the sine function to calculate the length of the sides.
For the 6-sided polygon above, if dimension D1 = 8'' : sin(30) = (S/2)/(8/2) =>sin(30) = S/8 =>.5 * 8 = S =>S = 4'' On the other hand, if we start the process knowing dimension D2 of the polygon, the length of each side of the shape can be calculated using the tangent function: tan(a) * A = S Beginning with the length of the sides (S), we can calculate dimension D1 using the sine function: sin(a)/S = D1 and similarly, using the tangent function we can calculate dimension D2: tan(a)/S = D2 The functions and methods used above can be used to find the angles and dimensions of any regular polygon, regardless of its size or number of sides. And with a little "mathematical creativity," they can be applied to any project where shapes can broken down into right triangles.
Using Math in Woodworking
If you're one of the many woodworkers who consistently avoid using mathematics to plan and build projects, we hope that this brief tour of the math used in angle calculations has shown you that the math used in woodworking isn't especially complicated. We also hope you noticed that the calculations we went through are based on only a few concepts from trigonometry. Just about every angle calculation problem you will ever encounter in woodworking can be worked through by applying the the functions and theorems discussed here. The more comfortable you are in applying mathematics to general woodworking situations, the more free you will be to pursue any project you choose.
Keep the inspiration coming!
Subscribe to our newsletter for more woodworking tips and tricks